本文共 6942 字,大约阅读时间需要 23 分钟。
注:本文是对《统计学习方法》EM算法的一个简单总结。
1. 什么是EM算法?
引用书上的话:
概率模型有时既含有观测变量,又含有隐变量或者潜在变量。如果概率模型的变量都是观测变量,可以直接使用极大似然估计法或者贝叶斯的方法进行估计模型参数,但是当模型含有隐藏变量时,就不能简单使用这些方法了。EM算法就是含有隐变量的概率模型参数的极大似然估计法,或者极大似然后验概率估计法。
2. EM 算法的一个小例子:三硬币模型
假设有3枚硬币,记作A,B,C。这些硬币的正面出现的概率分别为\(\pi\)、\(p\)、\(q\)。进行如下的试验:先掷硬币A,根据A的结果选择B和C,如果掷A得到正面,则选择B;如果掷A得到反面,则选择C。接着掷出选出的硬币。记录下这次掷硬币的结果,如果是正面,则记作1,反面则记作0。独立重复做了n次试验(这里取n=10),得到结果如下:1,1,0,1,0,0,1,0,1,1。假设只能观测到抛硬币的结果,不能观测到抛硬币的过程,那么我们该如何估计三硬币的参数\(\pi\)、\(p\)、\(q\)呢?(也就是估计三枚硬币正面向上的概率)
EM算法分为E步和M步。EM 算法首先选取了参数的初始值,记作\(\theta^{(0)}\)=(\(\pi^{(0)}\),\(p^{(0)}\),\(q^{(0)}\))。然后通过下面的步骤迭代计算参数的估计值,直到收敛为止,第\(i\)次迭代的参数的估计值记作\(\theta^{(i)}\)=(\(\pi^{(i)}\),\(p^{(i)}\),\(q^{(i)}\)),则EM算法的第\(i+1\)次迭代为: E步:计算模型在参数\(\pi^{(i)}\)、\(p^{(i)}\)、\(q^{(i)}\)下观测数据\(y_j\)来自掷硬币B的概率为\(\mu_j^{(i+1)}\) = \(\frac{\pi^{(i)}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j}}{\pi^{(i)}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j} + (1-\pi^{(i)})(q^{(i)})^{y_j}(1-q^{(i)})^{1-y_j}}\) M步:计算模型新的参数的估计值:\(\pi^{(i+1)}=\frac{1}{n}\sum_{j=1}^{n}\mu_j^{(i+1)}\)\(p^{(i+1)}=\frac{\sum_{j=1}^{n}\mu_j^{(i+1)}y_j}{\sum_{j=1}^{n}\mu_j^{(i+1)}}\)\(q^{(i+1)}=\frac{\sum_{j=1}^{n}(1-\mu_j^{(i+1)})y_j}{\sum_{j=1}^{n}(1-\mu_j^{(i+1)})}\)下面带入具体的数字计算一下。如果模型的初始参数取值为:\(\pi{(0)}=0.5,p^{(0)}=0.5,q^{(0)}=0.5\)
那么带入上面的三个公式就可以计算出:\(\pi{(1)}=0.5,p^{(1)}=0.6,q^{(1)}=0.6\),继续迭代可以得到 \(\pi{(2)}=0.5,p^{(2)}=0.6,q^{(2)}=0.6\)。于是我们可以得到原来参数\(\theta\)的极大似然估计为:\(\hat{\pi}=0.5,\hat{p}=0.6,\hat{q}=0.6\)。 如果取初值改为 \(\pi{(0)}=0.4,p^{(0)}=0.6,q^{(0)}=0.7\),那么我们可以计算出:\(\mu_1^{(1)}=\frac{0.4\times0.6}{0.4\times0.6+0.6\times0.7}=0.364\) :\(\mu_0^{(1)}=\frac{0.4\times0.4}{0.4\times0.4+0.6\times0.3}=0.47\) 那么由于观测值中1出现了6次,0出现了4次,于是我们容易计算出:\(\pi^{(1)}=\frac{0.364\times6+0.47\times4}{10}=0.4064\)\(p^{(1)}=\frac{0.364\times1\times6+0.47\times0\times4}{0.364\times6+0.47\times4}=0.537\)\(q^{(1)}=\frac{(1-0.364)\times6}{(1-0.364)\times6+(1-0.47)\times4}=0.643\) 显然,我们由于初始值选择的不同,导致了模型参数最终估计的不同,这说明了EM算法对于参数的初始值是非常敏感的。3 EM 算法的步骤
输入:观测变量数据\(Y\),隐变量数据\(Z\),联合分布\(P(Y,Z|\theta)\),条件分布\(P(Z|Y,\theta)\);
输出:模型参数\(\theta\)。(1) 选择模型参数的初值\(\theta^{(0)}\),开始迭代;
(2)\(E\)步:记\(\theta^{(i)}\)为第\(i\)次迭代参数\(\theta\)的估计值,在第\(i+1\)次迭代的E步,计算\(Q(\theta,\theta^{(i)}=E_Z[logP(Y,Z|\theta)|Y,\theta^{(i)}]=\sum_{Z}logP(Y,Z|\theta)P(Z|Y,\theta^{(i)})\) 这里\(P(Z|Y,\theta^{(i)})\)是在给定观测数据Y和当前参数估计的\(\theta^{(i)}\)下隐变量数据\(Z\)的条件概率分布; (3)\(M\)步:求使得\(Q(\theta,\theta^{(i)})\)极大化的\(\theta\),确定第\(i+1\)次迭代的参数的估计值\(\theta^{(i+1)}\)\(\theta^{(i+1)}=arg max_{\theta}Q(\theta,\theta^{(i)})\) (4)重复第(2)步和第(3)步,直到算法收敛。 上面定义的函数\(Q(\theta,\theta^{(i)})\)是EM算法的核心,称为Q函数(Q function)。下面给出Q函数的定义: (Q函数) 完全数据的对数似然函数\(logP(Y,Z|\theta)\)关于给定观测数据\(Y\)和当前参数\(\theta^{(i)}\)下对未观测数据\(Z\)的条件概率分布\(P(Z|Y,\theta^{(i)})\)的期望称为\(Q\)函数,即:\(Q(\theta,\theta^{(i)}=E_Z[logP(Y,Z|\theta)|Y,\theta^{(i)}]\)4. EM算法的收敛性
1. 设\(P(Y|\theta)\)为观测数据的似然函数,\(\theta^{(i)}(i=1,2,...)\)为EM算法得到的参数估计序列,\(P(Y|\theta^{(i)}\)为对应的似然函数序列,则\(P(Y|\theta^{(i)}\)是单调递增的,即:
\(P(Y|\theta^{(i+1)} \ge P(Y|\theta^{(i)})\)。
2. 设 \(L(\theta)=logP(Y|\theta)\)为观测数据的对数似然函数,\(\theta^{(i)}\)为EM算法得到的参数估计序列,\(L(\theta^{(i)})\)为对应的对数似然函数序列,则
(1) 如果\(P(Y|\theta)\)有上界,则\(L(\theta^{(i)})=logP(Y|\theta^{(i)})\)收敛到某一值\(L^{*}\);
(2) 在函数 \(Q(\theta,\theta^{'})\)与\(L(\theta)\)满足一定的条件下,由EM算法得到的参数估计序列\(\theta^{(i)}\)的收敛值\(\theta^{*}\)是\(L(\theta)\)的稳定点。
5. 高斯混合模型(GMM)
1. 高斯混合模型的定义:高斯混合模型是指具有如下形式的概率分布模型:
\(P(Y|\theta)=\sum_{k=1}^{K}\alpha_k\phi(y|\theta_k)\)
其中\(\alpha_k\)是系数,\(\alpha_k \ge 0\),\(\sum_{k=1}^{K}\alpha_k=1\);\(\phi(y|\theta_k)\)是高斯分布(正态分布)密度函数,\(\theta_k=(\mu_k,\sigma_k^{2})\),\(\phi(y|\theta_k)=\frac{1}{\sqrt(2\pi)\sigma_k}exp(-\frac{(y-\mu_k)^2}{2\sigma_k^2})\) 称为第\(k\)个分模型。2. 使用EM算法估计高斯混合模型
具体推导过程从略,可以参见《统计学习方法》。这里直接给出结果:
高斯混合模型的EM估计算法 输入:观测数据\(y_1,y_2,...,y_N\),高斯混合模型; 输出:高斯混合模型的参数。 (1)取参数的初始值迭代 (2)E步,依据当前模型的参数,计算分模型k对观测数据\(y_j\)的响应度,\(\hat\gamma_{jk}=\frac{\alpha_k\phi(y_j|\theta_k)}{\sum_{k=1}^{K}\alpha_k\phi(y_j|\theta_k)},j=1,2,...,N,k=1,2,...K\) (3)计算新一轮迭代的模型参数\(\hat\mu_k=\frac{\sum_{j=1}^{N}\hat\gamma_{jk}y_j}{\sum_{j=1}^{N}\hat\gamma_{jk}},k=1,2,...,K\)\(\hat\sigma_k^2=\frac{\sum_{j=1}^{N}\hat\gamma_{jk}(y_j-\mu_k)^2}{\sum_{j=1}^{N}\hat\gamma_{jk}},k=1,2,...,K\)\(\hat\alpha_k=\frac{\sum_{j=1}^{N}\hat\gamma_{jk}}{N},k=1,2,...,K\) (4)重复(2)和(3)直到收敛。6. python 实现 EM算法求解高斯混合模型
求解的步骤参考5,这里直接给出代码如下:
from __future__ import print_functionimport numpy as npdef generateData(k,mu,sigma,dataNum): ''' 产生混合高斯模型的数据 :param k: 比例系数 :param mu: 均值 :param sigma: 标准差 :param dataNum:数据个数 :return: 生成的数据 ''' # 初始化数据 dataArray = np.zeros(dataNum,dtype=np.float32) # 逐个依据概率产生数据 # 高斯分布个数 n = len(k) for i in range(dataNum): # 产生[0,1]之间的随机数 rand = np.random.random() Sum = 0 index = 0 while(index < n): Sum += k[index] if(rand < Sum): dataArray[i] = np.random.normal(mu[index],sigma[index]) break else: index += 1 return dataArraydef normPdf(x,mu,sigma): ''' 计算均值为mu,标准差为sigma的正态分布函数的密度函数值 :param x: x值 :param mu: 均值 :param sigma: 标准差 :return: x处的密度函数值 ''' return (1./np.sqrt(2*np.pi))*(np.exp(-(x-mu)**2/(2*sigma**2)))def em(dataArray,k,mu,sigma,step = 10): ''' em算法估计高斯混合模型 :param dataNum: 已知数据个数 :param k: 每个高斯分布的估计系数 :param mu: 每个高斯分布的估计均值 :param sigma: 每个高斯分布的估计标准差 :param step:迭代次数 :return: em 估计迭代结束估计的参数值[k,mu,sigma] ''' # 高斯分布个数 n = len(k) # 数据个数 dataNum = dataArray.size # 初始化gama数组 gamaArray = np.zeros((n,dataNum)) for s in range(step): for i in range(n): for j in range(dataNum): Sum = sum([k[t]*normPdf(dataArray[j],mu[t],sigma[t]) for t in range(n)]) gamaArray[i][j] = k[i]*normPdf(dataArray[j],mu[i],sigma[i])/float(Sum) # 更新 mu for i in range(n): mu[i] = np.sum(gamaArray[i]*dataArray)/np.sum(gamaArray[i]) # 更新 sigma for i in range(n): sigma[i] = np.sqrt(np.sum(gamaArray[i]*(dataArray - mu[i])**2)/np.sum(gamaArray[i])) # 更新系数k for i in range(n): k[i] = np.sum(gamaArray[i])/dataNum return [k,mu,sigma]if __name__ == '__main__': # 参数的准确值 k = [0.3,0.4,0.3] mu = [2,4,3] sigma = [1,1,4] # 样本数 dataNum = 5000 # 产生数据 dataArray = generateData(k,mu,sigma,dataNum) # 参数的初始值 # 注意em算法对于参数的初始值是十分敏感的 k0 = [0.3,0.3,0.4] mu0 = [1,2,2] sigma0 = [1,1,1] step = 6 # 使用em算法估计参数 k1,mu1,sigma1 = em(dataArray,k0,mu0,sigma0,step) # 输出参数的值 print("参数实际值:") print("k:",k) print("mu:",mu) print("sigma:",sigma) print("参数估计值:") print("k1:",k1) print("mu1:",mu1) print("sigma1:",sigma1) 运行结果如下:
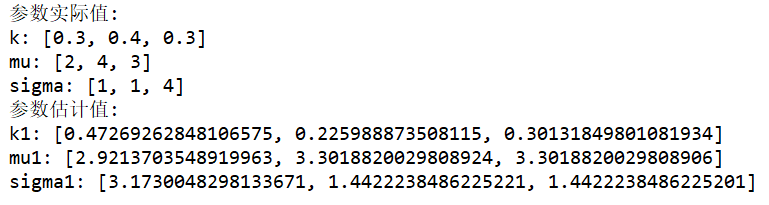 如果改变初始参数为:
如果改变初始参数为: k0=[0.1,0.4,0.5]mu0=[3,3,2]sigma0=[2,1,1.5]
那么得到的结果为:
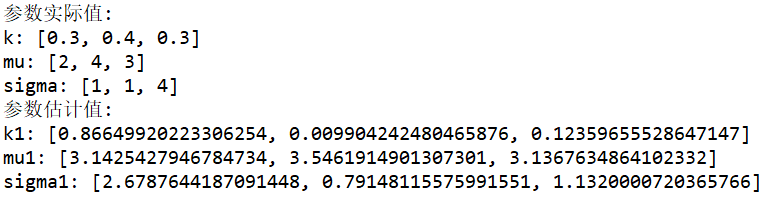 对比可以发现,两次参数估计的结果相差还是很大的。这也说明了EM算法对初始参数的敏感性。在实际应用的过程中,我们可以通过多次试验验证来选择估计结果最好的那个作为初始参数。 热爱编程,热爱机器学习! github:http://www.github.com/Lyrichu github blog:http://Lyrichu.github.io 个人博客站点:http://www.movieb2b.com(不再维护)
对比可以发现,两次参数估计的结果相差还是很大的。这也说明了EM算法对初始参数的敏感性。在实际应用的过程中,我们可以通过多次试验验证来选择估计结果最好的那个作为初始参数。 热爱编程,热爱机器学习! github:http://www.github.com/Lyrichu github blog:http://Lyrichu.github.io 个人博客站点:http://www.movieb2b.com(不再维护) 转载地址:http://kvcwo.baihongyu.com/